FUNCIONES CUADRÁTICAS

FUNCIONES CUADRÁTICAS

Ø ¿Qué es una función cuadrática?

Las funciones cuadráticas son aquellas funciones cuya expresión analítica sea la siguiente: F(x) = ax² + bx +c

Siendo a, b, c números reales,  y a diferente a 0.

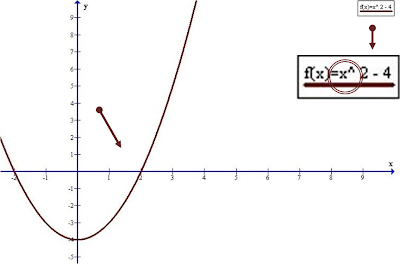
Ø ¿Qué es una parábola?

Es la representación gráfica en el plano cartesiano de una función cuadrática. 

Ø  Vértice y eje de simetría

Las parábolas son simétricas respecto a una recta vertical llamada eje de simetría.

 El punto en el que el eje corta la parábola se llama vértice. Este punto, dependiendo de la función, coincide con el máximo o el mínimo de la misma.

Ø  Análisis de la expresión analítica

Cuando el coeficiente principal tiene valor positivo, la parábola tiene concavidad positiva.

Cuando el coeficiente principal tiene valor negativo, la parábola tiene concavidad negativa.

Cuanto más grande sea el coeficiente principal  positivo, la parábola se acerca más a eje Y. 

De la misma manera, cuánto más chico sea el valor del coeficiente principal positivo, la parábola se acerca más al eje X.

Teniendo en cuenta la siguiente expresión analítica se pueden sacar ciertas conclusiones:

f(x) =(x-h) ^2

Si h es negativo, la gráfica se trasladara hacia la derecha. La misma se desplazará h unidades, desde el origen de los ejes, siendo -x el valor del coeficiente. 

Si h es positivo,  la gráfica se  trasladara hacia la izquierda. La misma se desplazará -h 

Unidades, desde el origen de los ejes, siendo x el valor del coeficiente.

   Máximo y mínimo

            -La abscisa  del mínimo, coincidirá con la raíz de la función.  

      

           -La ordenada del mínimo será siempre el opuesto a h, por lo tanto, la raíz también. 

      

          - Cuando la función tiene concavidad positiva, no tiene máximo.

          - Cuando la función tiene concavidad negativa, no tiene mínimo 

            

      Considerando la siguiente expresión analítica se pueden obtener ciertas conclusiones:

f(x) =(x-h)^2 + k

     

     - La coordenada x del vértice, coincidirá  h, mientras que la coordenada y del vértice será igual a k. 

       -El valor de k indicará cuántas unidades se desplazará la función sobre el eje y

    - Si k es mayor a 0, la función no tendrá raíz/ raíces. 

      -Si k=0, la función tiene una sola raíz (raíz doble)

               

 

Ángulos cóncavos.

 

Sin embargo, la definición de ángulo cóncavo es la siguiente: un ángulo es cóncavo, reflejo o entrante si mide más de 180° y menos de 360° rad y menos de  rad.

Figuras geométricas cóncavas

Un polígono es cóncavo, si al atravesarlo una recta puede cortarlo en más de dos puntos. Posee al menos un ángulo interior  cóncavo

.